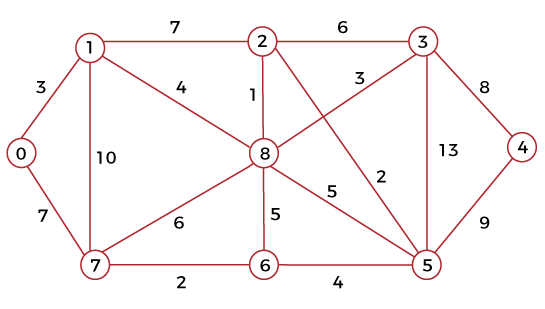
Dijkstra’s Algorithm#
Dijkstra’s algorithm is a famous algorithm for finding the shortest paths between nodes in a weighted graph. Imagine you have a map like a road network, where cities are represented by nodes and roads connecting them are the edges. Each road has a weight, which could be its distance, travel time, or cost. Dijkstra’s algorithm helps you find the most efficient route (shortest path) between two points on this map, considering the weights.
Here’s a simplified breakdown of how it works:
Start at a specific node (source): You choose a starting point on the map (source node).
Track distances: The algorithm keeps track of the tentative shortest distance from the source node to all other nodes. Initially, these distances are set to infinity, except for the source node itself (distance 0).
Explore neighbors: The algorithm examines the neighboring nodes of the source node. For each neighbor, it calculates the distance by traveling through the source node and adds that to the source’s distance to that neighbor.
Update and Repeat: If this calculated distance is shorter than the currently known distance to that neighbor, the algorithm updates the neighbor’s distance. Then, it picks the unvisited node with the shortest distance (tentatively the most promising path to explore) and repeats steps 3 and 4 for that node as the new center.
Shortest paths found: The algorithm continues exploring and updating distances until all nodes have been visited. At this point, the distances from the source node to all other nodes represent the shortest paths.
Dijkstra’s algorithm is widely used in various applications like GPS navigation systems, finding optimal routes in transportation networks, or planning efficient delivery paths.
Lecture Code Explanation#
This code implements Dijkstra’s algorithm to find the shortest paths from a single source vertex to all other vertices in a weighted graph. Here’s a breakdown of the code:
1. Class Dijkstra:
This class represents the core functionalities of Dijkstra’s algorithm.
It has properties like
totalVertexesto store the number of vertices in the graph andstartVertexto store the starting point for finding shortest paths.The constructor
Dijkstra(int totalVertexes)initializes these properties.
2. Utility methods:
minimumDistance(int distance[], boolean visited[]): This method finds the unvisited vertex with the minimum tentative distance from the source vertex. It iterates through thedistancearray and thevisitedarray to find the closest unvisited vertex.printSolution(int distance[], int n): This method prints the calculated shortest distances from the source vertex to all other vertices. It iterates through thedistancearray and prints the distance for each vertex.
3. calculate(int graph[][], int startVertex, int totalVertexes):
This is the main method that implements Dijkstra’s algorithm.
It takes the adjacency matrix representation of the graph (
graph), the starting vertex (startVertex), and the total number of vertices (totalVertexes) as input.It initializes two arrays:
distanceto store the tentative distances from the source vertex, andvisitedto keep track of visited vertices.It sets all distances in the
distancearray to infinity (except the source vertex which is set to 0).It iterates
totalVertexes-1
times (because we need to find shortest paths to all vertices):
In each iteration, it finds the unvisited vertex with the minimum tentative distance from the source vertex using
minimumDistance.It marks the found vertex as visited.
It iterates through all unvisited neighbors of the visited vertex.
For each neighbor, it calculates the tentative distance if going through the visited vertex is shorter than the current tentative distance.
If the new tentative distance is shorter, it updates the distance in the
distancearray.
Finally, it calls
printSolutionto print the calculated shortest distances.
4. Main method:
This method creates a sample adjacency matrix representing a weighted graph.
It creates an instance of the
Dijkstraclass (dgrpah) with the number of vertices in the graph (9).It calls the
calculatemethod of thedgrpahobject, providing the graph, starting vertex (8), and total vertices (9).
Overall, this code demonstrates how to implement Dijkstra’s algorithm to find the shortest paths in a weighted graph.
int minimumDistance(int distance[], boolean visited[])#
This code snippet implements the minimumDistance function within the Dijkstra’s algorithm class. Here’s a breakdown of what it does:
1. Finding the Unvisited Vertex with Minimum Tentative Distance:
It initializes two variables:
m: This variable stores the current minimum tentative distance found so far. It’s initialized to the maximum integer value (Integer.MAX_VALUE) to ensure the first encountered unvisited vertex becomes the initial minimum.m_index: This variable stores the index of the vertex with the minimum tentative distance. It’s initialized to -1 to indicate no vertex found yet.
The code iterates through all vertices in the graph using a loop (
for(int vx= 0; vx < totalVertexes; vx++)).Inside the loop, it checks two conditions for each vertex (
vx):visited[vx] == false: This condition checks if the vertex is not yet visited. We only care about unvisited vertices because we’re looking for the next closest unvisited point to explore.distance[vx] <= m: This condition checks if the current tentative distance of the vertex (distance[vx]) is less than or equal to the current minimum distance (m).
If both conditions are true, it means we found an unvisited vertex with a tentative distance that’s either smaller than or equal to the current minimum. In this case:
The value of
distance[vx](the vertex’s tentative distance) is assigned tom, updating the current minimum.The index of the vertex (
vx) is assigned tom_index, keeping track of the vertex with the current minimum tentative distance.
2. Returning the Index of the Minimum Distance Vertex:
After iterating through all vertices, the
m_indexwill hold the index of the unvisited vertex with the minimum tentative distance from the source vertex (or -1 if no unvisited vertices were found).Finally, the function returns the
m_index.
In summary, this function finds the unvisited vertex in the graph with the closest (minimum tentative distance) to the source vertex among all unvisited vertices. This vertex becomes the next point to explore in Dijkstra’s algorithm for finding the shortest paths.
This code snippet iterates through the unvisited neighbors of a vertex (ux) in Dijkstra’s algorithm and updates the tentative distances of those neighbors if necessary. Here’s a breakdown of what it does:
for(int vx = 0; vx <totalVertexes; vx++)
{
if(!visited[vx] && graph[ux][vx] != -1 &&
distance[ux] + graph[ux][vx] != Integer.MAX_VALUE &&
distance[ux] + graph[ux][vx] < distance[vx] )
{
distance[vx]= distance[ux] + graph[ux][vx];
}
}
1. Looping through Unvisited Neighbors:
The code uses a loop (
for(int vx = 0; vx <totalVertexes; vx++)) to iterate through all vertices (vx) in the graph.
2. Checking Conditions for Neighbor Update:
Inside the loop, it checks four conditions to determine if the tentative distance of the current neighbor (
vx) needs to be updated:!visited[vx]: This condition checks if the neighbor (vx) is not visited. We only care about unvisited neighbors because we’re exploring possible paths through the graph.graph[ux][vx] != -1: This condition checks if there’s an edge (connection) between the current vertex (ux) and the neighbor (vx) in the graph. A value of -1 in the adjacency matrix typically represents no connection.distance[ux] + graph[ux][vx] != Integer.MAX_VALUE: This condition checks if adding the tentative distance of the current vertex (distance[ux]) and the weight of the edge betweenuxandvx(graph[ux][vx]) doesn’t overflow to infinity. This ensures we don’t encounter invalid distances.distance[ux] + graph[ux][vx] < distance[vx]: This is the most important condition. It checks if the tentative distance from the source vertex to the current neighbor (vx) going through the current vertex (ux) is shorter than the current tentative distance of the neighbor (distance[vx]).
3. Updating Tentative Distance:
If all four conditions are true, it means we found a shorter path to the neighbor (
vx) by going through the current vertex (ux). In this case:The new tentative distance is calculated by adding the tentative distance of the current vertex (
distance[ux]) and the weight of the edge between them (graph[ux][vx]).This new tentative distance is assigned to
distance[vx], effectively updating the tentative distance of the neighbor in thedistancearray.
In summary, this code snippet iterates through the unvisited neighbors of a vertex and updates the tentative distances of those neighbors if going through the current vertex provides a shorter path. This is a crucial step in Dijkstra’s algorithm for finding the shortest paths from a source vertex to all other vertices in the graph.
Lecture Code#
/*
Project: Dijkstra's Algorithm
Programmer: James Goudy
*/
/*
*/
package ds_dijstraka_demo;
class Dijkstra {
// Number of vertices in the graph
int totalVertexes;
// Starting vertex for finding shortest paths
int startVertex;
public Dijkstra(int totalVertexes) {
this.totalVertexes = totalVertexes;
}
// Finds the unvisited vertex with the minimum tentative distance from the source vertex
int minimumDistance(int distance[], boolean visited[]) {
// Initialize minimum value
int m = Integer.MAX_VALUE;
int m_index = -1;
for (int vx = 0; vx < totalVertexes; vx++) {
// Check if vertex is unvisited and has a tentative distance less than or equal to current minimum
if (!visited[vx] && distance[vx] <= m) {
m = distance[vx];
m_index = vx;
}
}
return m_index;
}
// Utility function to print the calculated shortest distances
void printSolution(int distance[], int n) {
System.out.println(String.format("The shortest distance from source %1$sth node\nto all of the other nodes are: \n", n));
for (int i = 0; i < n; i++) {
System.out.println(n + " To " + i + " the shortest distance is : " + distance[i]);
}
System.out.println("\n-----------\n\n");
}
// Main function to calculate Dijkstra's shortest paths
void calculate(int graph[][], int startVertex, int totalVertexes) {
this.totalVertexes = totalVertexes;
this.startVertex = startVertex;
// Arrays to store tentative distances and visited status for vertices
int distance[] = new int[totalVertexes];
boolean visited[] = new boolean[totalVertexes];
// Initialize all distances as infinite (except the starting vertex which is 0)
for (int j = 0; j < totalVertexes; j++) {
distance[j] = Integer.MAX_VALUE;
}
distance[startVertex] = 0;
// Find shortest paths for all vertices iteratively
for (int c = 0; c < totalVertexes - 1; c++) {
// Get the unvisited vertex with the minimum tentative distance from the source vertex
int ux = minimumDistance(distance, visited);
visited[ux] = true; // Mark the vertex as visited
// Iterate through unvisited neighbors of the visited vertex
for (int vx = 0; vx < totalVertexes; vx++) {
// Check conditions to update tentative distance of the neighbor
if (!visited[vx] && graph[ux][vx] != -1 &&
distance[ux] + graph[ux][vx] != Integer.MAX_VALUE &&
distance[ux] + graph[ux][vx] < distance[vx]) {
distance[vx] = distance[ux] + graph[ux][vx]; // Update tentative distance
}
}
}
// Print the calculated shortest distances
printSolution(distance, totalVertexes);
}
}
public class DS_Dijstraka_Demo {
public static void main(String[] args) {
int graph[][] = new int[][]{
{-1, 3,-1,-1,-1,-1,-1, 7,-1},
{ 3,-1, 7,-1,-1,-1,-1,10, 4},
{-1, 7,-1, 6,-1, 2,-1,-1, 1},
{-1,-1, 6,-1, 8,13,-1,-1, 3},
{-1,-1,-1, 8,-1, 9,-1,-1,-1},
{-1,-1, 2,13, 9,-1, 4,-1, 5},
{-1,-1,-1,-1,-1, 4,-1, 2, 5},
{ 7,10,-1,-1,-1,-1, 2,-1, 6},
{-1, 4, 1, 3,-1, 5, 5, 6,-1}
};
Dijkstra dgrpah = new Dijkstra(9);
dgrpah.calculate(graph, 8,9);
}
}
}